Chapter 10 Matrix Factorizations
In scalar mathematics, a factorization is an expression that writes a scalar \(a\) as a product of two or more scalars. For example, the scalar 2 has a square-root factorization of \(2 =\sqrt{2} * \sqrt{2}\) and 15 has a prime factorization of \(15 = 3 * 5\). A matrix factorization is a similar concept where a matrix \(\mathbf{A}\) can be represented by a product or two or more matrices (e.g., \(\mathbf{A} = \mathbf{B} \mathbf{C}\)). In data science, matrix factorizations are fundamental to working with data.
10.1 The LU factorization
First, we define lower and upper triangular matrices.
Definition 10.1 The matrix \(\mathbf{A}\) is said to be lower triangular if
\[
\begin{aligned}
\mathbf{A} = \begin{pmatrix}
a_{11} & 0 & 0 & \cdots & 0 \\
a_{21} & a_{22} & 0 & \cdots & 0 \\
a_{31} & a_{32} & a_{33} & \cdots & 0 \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
a_{n1} & a_{n2} & a_{n3} & \cdots & a_{nn} \\
\end{pmatrix}
\end{aligned}
\]
Similarly, the matrix \(\mathbf{A}\) is said to be upper triangular if
\[
\begin{aligned}
\mathbf{A} = \begin{pmatrix}
a_{11} & a_{12} & a_{13} & \cdots & a_{1n} \\
0 & a_{22} & a_{23} & \cdots & a_{2n} \\
0 & 0 & a_{33} & \cdots & a_{3n} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
0 & 0 & 0 & \cdots & a_{nn} \\
\end{pmatrix}
\end{aligned}
\]
The LU factorization of a matrix \(\mathbf{A}\) reduces the matrix \(\mathbf{A}\) into two components. The first component \(\mathbf{L}\) is a lower-triangular matrix and the second component \(\mathbf{U}\) is an upper triangular matrix.
Using the LU factorization, the matrix factorization \(\mathbf{A} = \mathbf{L} \mathbf{U}\) can be used in the matrix equation \(\mathbf{A} \mathbf{x} = \mathbf{L} \mathbf{U}\mathbf{x} = \mathbf{b}\) by first solving the sub-equation \(\mathbf{L} \mathbf{y} = \mathbf{b}\) and then solving the second sub-equation \(\mathbf{U} \mathbf{x} = \mathbf{y}\) for \(\mathbf{x}\). Thus, the matrix factorization applied to the matrix equation gives the pair of equations
\[ \begin{aligned} \mathbf{L} \mathbf{y} & = \mathbf{b} \\ \mathbf{U} \mathbf{x} & = \mathbf{y} \end{aligned} \tag{10.1} \]
At first glance, this seems like we are trading the challenge of solving one system of equations \(\mathbf{A}\mathbf{x}\) (6.1) for the two equations in (10.1). However, the computational benefits arise due to the fact that \(\mathbf{L}\) and \(\mathbf{U}\) are triangular matrices and solving matrix equations with triangular matrices is much faster.
Example 10.1 Let \(\mathbf{A} = \begin{pmatrix} 1 & 0 & 2 & -2 \\ -2 & -2 & -4 & 1 \\ -1 & -4 & -8 & 5 \\ -2 & -6 & -4 & 4 \end{pmatrix}\) which has the LU decomposition
\[ \begin{aligned} \mathbf{A} = \begin{pmatrix} 1 & 0 & 2 & -2 \\ -2 & -2 & -4 & 1 \\ -1 & -4 & -8 & 5 \\ -2 & -6 & -4 & 4 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 & 0 \\ -2 & -1 & 0 & 0 \\ -1 & -2 & -3 & 0 \\ -2 & -3 & 0 & -3 \end{pmatrix} \begin{pmatrix} 1 & 0 & 2 & -2 \\ 0 & 2 & 0 & 3 \\ 0 & 0 & 2 & -3 \\ 0 & 0 & 0 & -3 \end{pmatrix} \end{aligned} \] and consider the system of equations defined by the matrix equation \(\mathbf{A} \mathbf{x} = \mathbf{b}\) where \(\mathbf{b} = \begin{pmatrix} -5 \\ -7 \\ -2 \\ -14 \end{pmatrix}\).
solve \(\mathbf{L} \mathbf{y} = \mathbf{b}\) using an augmented matrix and RREF.
solve \(\mathbf{U} \mathbf{x} = \mathbf{y}\) using an augmented matrix and RREF.
compare to the solution \(\mathbf{A}\mathbf{x} = \mathbf{b}\) using an augmented matrix and RREF.
Solution. For the example, we will show how to solve a system of equations using the LU decomposition for the equation defined above.
- Solve \(\mathbf{L} \mathbf{y} = \mathbf{b}\) using augmented matrix
\[ \begin{aligned} & & \begin{pmatrix} 1 & 0 & 0 & 0 & -5 \\ -2 & -1 & 0 & 0 & -7 \\ -1 & -2 & -3 & 0 & -2 \\ -2 & -3 & 0 & -3 & -14 \end{pmatrix} & \stackrel{r_2 \leftarrow -\frac{1}{2} r_2 - r_1}{\huge \sim} & \begin{pmatrix} 1 & 0 & 0 & 0 & -5 \\ 0 & 1/2 & 0 & 0 & 17/2 \\ -1 & -2 & -3 & 0 & -2 \\ -2 & -3 & 0 & -3 & -14 \end{pmatrix} \\ & \stackrel{r_3 \leftarrow - r_3 - r_1}{\huge \sim} & \begin{pmatrix} 1 & 0 & 0 & 0 & -5 \\ 0 & 1/2 & 0 & 0 & 17/2 \\ 0 & 2 & 3 & 0 & 7 \\ -2 & -3 & 0 & -3 & -14 \end{pmatrix} & \stackrel{r_4 \leftarrow - \frac{1}{2} r_4 - r_1}{\huge \sim} & \begin{pmatrix} 1 & 0 & 0 & 0 & -5 \\ 0 & 1/2 & 0 & 0 & 17/2 \\ 0 & 2 & 3 & 0 & 7 \\ 0 & 3/2 & 0 & 3/2 & 12 \end{pmatrix} \\ & \stackrel{r_2 \leftarrow 2 r_2}{\huge \sim} & \begin{pmatrix} 1 & 0 & 0 & 0 & -5 \\ 0 & 1 & 0 & 0 & 17 \\ 0 & 2 & 3 & 0 & 7 \\ 0 & 3/2 & 0 & 3/2 & 12 \end{pmatrix} & \stackrel{r_3 \leftarrow \frac{1}{2} r_3 - r_2}{\huge \sim} & \begin{pmatrix} 1 & 0 & 0 & 0 & -5 \\ 0 & 1 & 0 & 0 & 17 \\ 0 & 0 & 3/2 & 0 & -27/2 \\ 0 & 3/2 & 0 & 3/2 & 12 \end{pmatrix} \\ & \stackrel{r_4 \leftarrow \frac{2}{3} r_4 - r_2}{\huge \sim} & \begin{pmatrix} 1 & 0 & 0 & 0 & -5 \\ 0 & 1 & 0 & 0 & 17 \\ 0 & 0 & 3/2 & 0 & -27/2 \\ 0 & 0 & 0 & 1 & -9 \end{pmatrix} & \stackrel{r_3 \leftarrow \frac{2}{3} r_3}{\huge \sim} & \begin{pmatrix} 1 & 0 & 0 & 0 & -5 \\ 0 & 1 & 0 & 0 & 17 \\ 0 & 0 & 1 & 0 & -9 \\ 0 & 0 & 0 & 1 & -9 \end{pmatrix} \end{aligned} \]
- solve \(\mathbf{U} \mathbf{x} = \mathbf{y}\) using an augmented matrix and RREF.
\[ \begin{aligned} & & \begin{pmatrix} 1 & 0 & 2 & -2 & -5 \\ 0 & 2 & 0 & 3 & 17 \\ 0 & 0 & 2 & -3 & -9 \\ 0 & 0 & 0 & -3 & -9 \end{pmatrix} & \stackrel{r_2 \leftarrow \frac{1}{2} r_2}{\huge \sim} & \begin{pmatrix} 1 & 0 & 2 & -2 & -5 \\ 0 & 1 & 0 & 3/2 & 17/2 \\ 0 & 0 & 2 & -3 & -9 \\ 0 & 0 & 0 & -3 & -9 \end{pmatrix} \\ & \stackrel{r_3 \leftarrow \frac{1}{2} r_3}{\huge \sim} & \begin{pmatrix} 1 & 0 & 2 & -2 & -5 \\ 0 & 1 & 0 & 3/2 & 17/2 \\ 0 & 0 & 1 & -3/2 & -9/2 \\ 0 & 0 & 0 & -3 & -9 \end{pmatrix} & \stackrel{r_4 \leftarrow - \frac{1}{3} r_4}{\huge \sim} & \begin{pmatrix} 1 & 0 & 2 & -2 & -5 \\ 0 & 1 & 0 & 3/2 & 17/2 \\ 0 & 0 & 1 & -3/2 & -9/2 \\ 0 & 0 & 0 & 1 & 3 \end{pmatrix} \\ & \stackrel{r_1 \leftarrow r_1 -2 r_3}{\huge \sim} & \begin{pmatrix} 1 & 0 & 0 & 1 & 4 \\ 0 & 1 & 0 & 3/2 & 17/2 \\ 0 & 0 & 1 & -3/2 & -9/2 \\ 0 & 0 & 0 & 1 & 3 \end{pmatrix} & \stackrel{r_1 \leftarrow r_1 - 2 r_4}{\huge \sim} & \begin{pmatrix} 1 & 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 3/2 & 17/2 \\ 0 & 0 & 1 & -3/2 & -9/2 \\ 0 & 0 & 0 & 1 & 3 \end{pmatrix} \\ & \stackrel{r_2 \leftarrow r_2 - \frac{3}{2} r_4}{\huge \sim} & \begin{pmatrix} 1 & 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 & 4 \\ 0 & 0 & 1 & -3/2 & -9/2 \\ 0 & 0 & 0 & 1 & 3 \end{pmatrix} & \stackrel{r_3 \leftarrow r_3 + \frac{3}{2} r_4}{\huge \sim} & \begin{pmatrix} 1 & 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 & 4 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 3 \end{pmatrix} \end{aligned} \]
- compare to the solution \(\mathbf{A}\mathbf{x} = \mathbf{b}\) using an augmented matrix and RREF.
\[ \begin{aligned} & & \begin{pmatrix} 1 & 0 & 2 & -2 & -5 \\ -2 & -2 & -4 & 1 & -7 \\ -1 & -4 & -8 & 5 & -2 \\ -2 & -6 & -4 & 4 & -14 \end{pmatrix} & \stackrel{r_2 \leftarrow r_2 + 2 r_1}{\huge \sim} & \begin{pmatrix} 1 & 0 & 2 & -2 & -5 \\ 0 & -2 & 0 & -3 & -17 \\ -1 & -4 & -8 & 5 & -2 \\ -2 & -6 & -4 & 4 & -14 \end{pmatrix} \\ & \stackrel{r_3 \leftarrow r_3 + r_1}{\huge \sim} & \begin{pmatrix} 1 & 0 & 2 & -2 & -5 \\ 0 & -2 & 0 & -3 & -17 \\ 0 & -4 & -6 & 3 & -7 \\ -2 & -6 & -4 & 4 & -14 \end{pmatrix} & \stackrel{r_4 \leftarrow r_4 + 2 r_1}{\huge \sim} & \begin{pmatrix} 1 & 0 & 2 & -2 & -5 \\ 0 & -2 & 0 & -3 & -17 \\ 0 & -4 & -6 & 3 & -7 \\ 0 & -6 & 0 & 0 & -24 \end{pmatrix} \\ & \stackrel{r_2 \leftarrow - \frac{1}{2} r_2}{\huge \sim} & \begin{pmatrix} 1 & 0 & 2 & -2 & -5 \\ 0 & 1 & 0 & 3/2 & 17/2 \\ 0 & -4 & -6 & 3 & -7 \\ 0 & -6 & 0 & 0 & -24 \end{pmatrix} & \stackrel{r_3 \leftarrow r_3 + 4 r_2}{\huge \sim} & \begin{pmatrix} 1 & 0 & 2 & -2 & -5 \\ 0 & 1 & 0 & 3/2 & 17/2 \\ 0 & 0 & -6 & 9 & 27 \\ 0 & -6 & 0 & 0 & -24 \end{pmatrix} \\ & \stackrel{r_4 \leftarrow r_4 + 6 r_2}{\huge \sim} & \begin{pmatrix} 1 & 0 & 2 & -2 & -5 \\ 0 & 1 & 0 & 3/2 & 17/2 \\ 0 & 0 & -6 & 9 & 27 \\ 0 & 0 & 0 & 9 & 27 \end{pmatrix} & \stackrel{r_3 \leftarrow - \frac{1}{6} r_3}{\huge \sim} & \begin{pmatrix} 1 & 0 & 2 & -2 & -5 \\ 0 & 1 & 0 & 3/2 & 17/2 \\ 0 & 0 & 1 & -3/2 & -9/2 \\ 0 & 0 & 0 & 9 & 27 \end{pmatrix}\\ & \stackrel{r_4 \leftarrow \frac{1}{9} r_4}{\huge \sim} & \begin{pmatrix} 1 & 0 & 2 & -2 & -5 \\ 0 & 1 & 0 & 3/2 & 17/2 \\ 0 & 0 & 1 & -3/2 & -9/2 \\ 0 & 0 & 0 & 1 & 3 \end{pmatrix} & \stackrel{r_1 \leftarrow r_1 - 2 r_3}{\huge \sim} & \begin{pmatrix} 1 & 0 & 0 & 1 & 4 \\ 0 & 1 & 0 & 3/2 & 17/2 \\ 0 & 0 & 1 & -3/2 & -9/2 \\ 0 & 0 & 0 & 1 & 3 \end{pmatrix} \\ & \stackrel{r_1 \leftarrow r_1 - r_4}{\huge \sim} & \begin{pmatrix} 1 & 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 3/2 & 17/2 \\ 0 & 0 & 1 & -3/2 & -9/2 \\ 0 & 0 & 0 & 1 & 3 \end{pmatrix} & \stackrel{r_2 \leftarrow r_2 - \frac{3}{2} r_4}{\huge \sim} & \begin{pmatrix} 1 & 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 & 4 \\ 0 & 0 & 1 & -3/2 & -9/2 \\ 0 & 0 & 0 & 1 & 3 \end{pmatrix} \\ & \stackrel{r_3 \leftarrow r_3 + \frac{3}{2} r_4}{\huge \sim} & \begin{pmatrix} 1 & 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 & 4 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 3 \end{pmatrix} \end{aligned} \]
While it might not be completely obvious, once one has calculated the LU decomposition, it can often be much faster to solve systems of equations with the LU decomposition.
Exercise 10.1 in lab: Solve some large systems of equations by brute force which shows how the LU decomposition is faster.
10.1.1 Geometric interpretation of the LU factorization
- Draw image in class – composition of transformations \(T_A(\cdot) = T_L(T_U(\cdot))\)
10.2 Obtaining the LU factorization
Notice that the upper-triangular matrix \(\mathbf{U}\) is in echelon form. Congratulations! you know how to construct a matrix \(\mathbf{U}\) by reducing the matrix \(\mathbf{A}\) to an echelon form \(\mathbf{U}\) using elementary matrices \(\mathbf{E}_1, \ldots \mathbf{E}_k\). Now, we only need to find the lower triangular matrix \(\mathbf{L}\).
Combining the LU factorization and the fact that we can find an upper triangular matrix \(\mathbf{U}\) using elementary row matrices, we have
\[ \begin{aligned} \mathbf{A} & = \mathbf{L} \mathbf{U} \\ \mathbf{E}_k \cdots \mathbf{E}_1 \mathbf{A} & = \mathbf{U}. \end{aligned} \tag{10.2} \] We also know that each of the elementary row matrices \(\mathbf{E}_j\) are invertible (you can always re-swap rows, subtract instead of add rows, etc.) which says that each inverse \(\mathbf{E}_j^{-1}\) exists. Thus, the product \(\mathbf{E}_k \cdots \mathbf{E}_1\) must have an inverse which is \[ \begin{aligned} (\mathbf{E}_k \cdots \mathbf{E}_1)^{-1} & = \mathbf{E}_1^{-1} \cdots \mathbf{E}_k^{-1}. \end{aligned} \] Plugging this inverse into (10.2) gives (left multiplying by \((\mathbf{E}_k \cdots \mathbf{E}_1)^{-1}\) on both sides) \[ \begin{aligned} (\mathbf{E}_k \cdots \mathbf{E}_1)^{-1} (\mathbf{E}_k \cdots \mathbf{E}_1) \mathbf{A} & = (\mathbf{E}_k \cdots \mathbf{E}_1)^{-1}\mathbf{U} \\ \mathbf{A} & = (\mathbf{E}_k \cdots \mathbf{E}_1)^{-1}\mathbf{U} \\ & = \mathbf{L} \mathbf{U} \end{aligned} \] where \(\mathbf{L} = (\mathbf{E}_k \cdots \mathbf{E}_1)^{-1}\)
Algorithm for finding the LU decomposition
Given the matrix \(\mathbf{A}\)
Find elementary matrices \(\mathbf{E}_1, \ldots, \mathbf{E}_k\) such that \(\mathbf{E}_k \cdots \mathbf{E}_1 \mathbf{A}\) is in row echelon form (if this is possible, otherwise an LU factorization does not exist). Call this matrix \(\mathbf{U}\), the upper triangular component of the LU factorization.
The, the lower triangular \(\mathbf{L} = (\mathbf{E}_k \cdots \mathbf{E}_1)^{-1}\).
Notice that the algorithm does not say to find a specific matrix \(\mathbf{U}\). In general, any row echelon form matrix \(\mathbf{U}\) will work.
10.3 The Cholesky factor
A Cholesky decomposition is special type of LU decomposition. A Cholesky decomposition is an LU decomposition on a symmetric, positive-definite square matrix.
A matrix \(\mathbf{A}\) is said to by symmetric if \(\mathbf{A} = \mathbf{A}'\)
A \(n \times n\) matrix is said to be positive definite if for all \(\mathbf{x} \in \mathcal{R}^n\), the quadratic form \(\mathbf{x}' \mathbf{A }\mathbf{x} \geq 0\)
Note: the condition of positive definiteness is actually impossible to check. Can you show this is true for all vectors? Luckily, a \(n \times n\) symmetric matrix is positive definite if and only if the matrix \(\mathbf{A}\) is invertible (which we know about by the invertible matrix theorem 9.4).
Definition 10.2 Let \(\mathbf{A}\) be a symmetric, positive definite matrix (by this, \(\mathbf{A}\) is a \(n \times n\) square matrix). Then \[ \begin{aligned} \mathbf{A} = \mathbf{L} \mathbf{L}' \end{aligned} \] is the Cholesky decomposition of \(\mathbf{A}\) if \(\mathbf{L}\) is a lower-triangular matrix. Also, the lower triangular Cholesky matrix \(\mathbf{L}\) is unique.
What makes the Cholesky factor special?
The decomposition \(\mathbf{A} = \mathbf{L} \mathbf{U}\) has the property that \(\mathbf{U} = \mathbf{L}'\) so that the computer only has to store one of the matrix components (reduce memory demands). As about half of the elements of \(\mathbf{L}\) are 0, matrix multiplication is much less computationally demanding as about half of the flops are not required to be evaluated (x * 0 = 0).
The Cholesky factor is unique. There is only one Cholesky factor for each symmetric positive definite matrix.
The Cholesky has properties related to multivariate normal distributions.
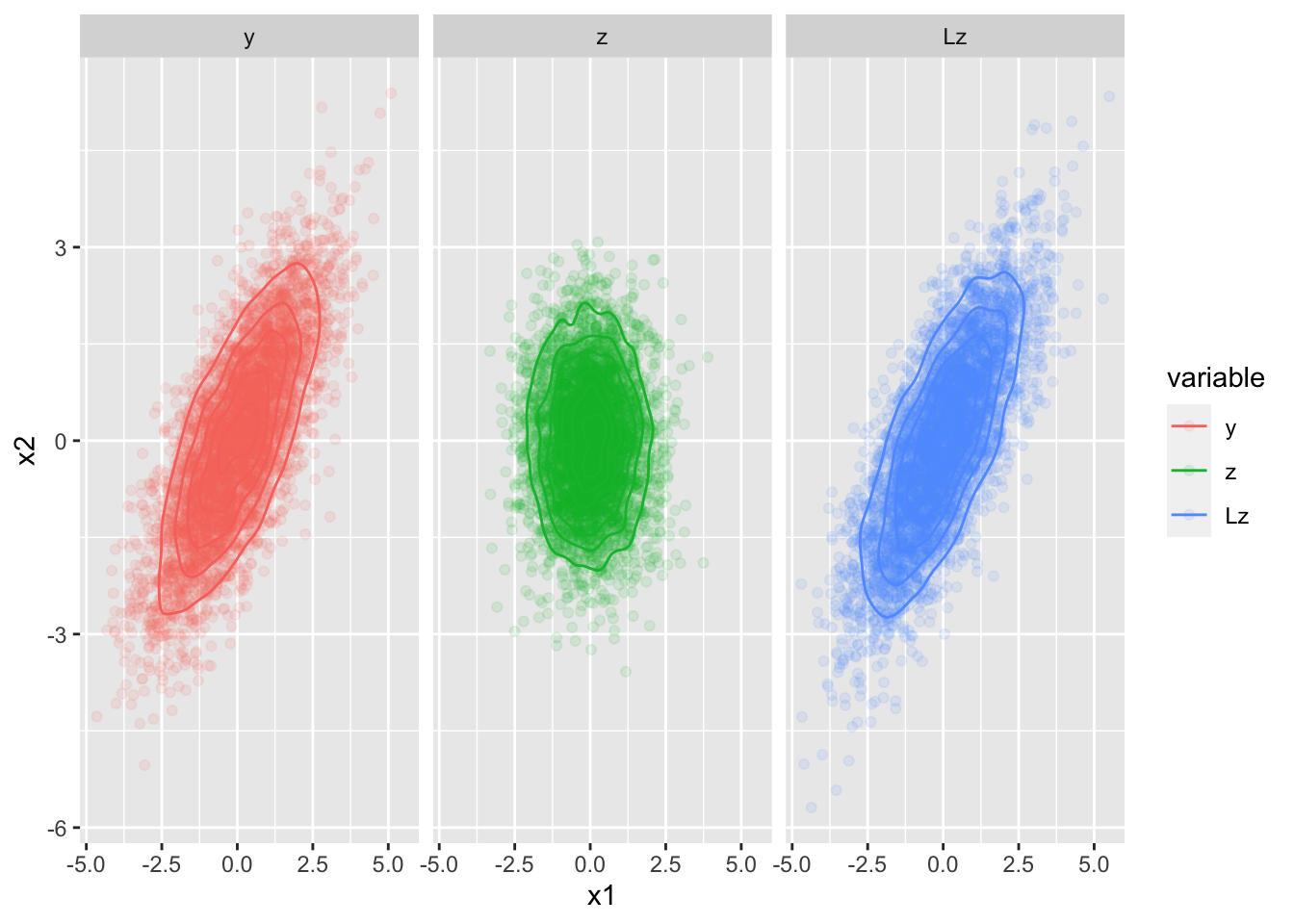
Let \(\mathbf{y} \sim \operatorname{N}(\mathbf{0}, \boldsymbol{\Sigma})\), and \(\boldsymbol{\Sigma} = \mathbf{L} \mathbf{L}'\). Then, if \(\mathbf{z} \sim \operatorname{N}(\mathbf{0}, \mathbf{I})\), then \(\mathbf{L} \mathbf{z} \sim \operatorname{N}(\mathbf{0}, \boldsymbol{\Sigma})\). We say the \(\mathbf{y}\) and \(\mathbf{L}\mathbf{z}\) are equal in distribution.
# simulate N 2-dimensional random normal vectors
N <- 5000
mu <- rep(0, 2)
Sigma <- matrix(c(2, 1.5, 1.5, 2), 2, 2)
y <- rmvn(N, mu, Sigma)
# calculate the Cholesky factor
L <- t(chol(Sigma)) # R calculates the upper (right) Cholesky factor by default
z <- rmvn(N, mu, diag(2))
Lz <- t(L %*% t(z)) # pay attention to the dimensions of L and z here...
data.frame(
observation = 1:N,
x1 = c(y[, 1], z[, 1], Lz[, 1]),
x2 = c(y[, 2], z[, 2], Lz[, 2]),
variable = factor(rep(c("y", "z", "Lz"), each = N), levels = c("y", "z", "Lz"))
) %>%
ggplot(aes(x = x1, y = x2, color = variable)) +
geom_point(alpha = 0.1) +
geom_density2d() +
facet_wrap(~ variable)